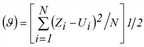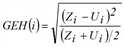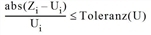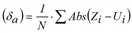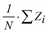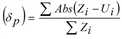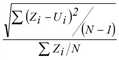Umlegungsanalyse IV

Die Umlegungsanalyse dient der Berechnung der Korrelation (Goodness-of-Fit Report) zwischen berechneten und beobachteten Werten von Attributen eines ausgewählten Netzobjekttyps.

Der berechnete Wert stammt aus der Umlegung oder dem Netzmodell.
Der beobachtete Wert kann ein Zähl- oder Messwert sein.

Hier sind einige Anwendungsbeispiele.

Reisezeitvergleiche zwischen IV und ÖV
Reisezeitvergleiche verschiedener Szenarien
Berechnete und gezählte Belastungen (Strecken, Abbieger oder Oberabbieger)
Berechnete und gemessene Geschwindigkeiten

Zur Auswahl stehen alle numerischen Eingabe- und Ausgabe-Attribute der folgenden Netzobjekttypen:

Strecken
Knoten
Abbieger
Oberknoten
Oberabbieger
Linien
Linienrouten
Screenlines
Fahrzeitprofile
Wege

Voraussetzung ist, dass die beobachteten Werte >0 sein müssen für den gewählten Netzobjekttyp.

Sie können wählen, welche Objekte Sie in die Umlegungsanalyse einbeziehen wollen. Es bestehen drei Möglichkeiten.

Alle Objekte des gewählten Netzobjekttyps
Nur aktive Objekte
Nur Objekte mit beobachtetem Wert > 0.

Optional können Sie bei der Umlegungsanalyse benutzerdefinierte Toleranzen für benutzerdefinierte Werteklassen des berechneten Attributs berücksichtigen.

Die Güte der Korrelation kann auf zwei Arten ermittelt und ausgegeben werden.

Gruppiert (je Wert des Klassifizierungsattributs)
Insgesamt für alle einbezogenen Netzobjekte

Für die Ausgabe wurde das Datenmodell für die oben genannten Netzobjekttypen erweitert um das berechnete Attribut Umlegungsabweichung (UmlgAbw / ASSIGNDEVIATION) vom Typ Real, das wie alle anderen Visum-Attribute für das jeweilige Netzobjekt grafisch und tabellarisch dargestellt werden kann.

Darüber hinaus werden diverse Kenngrößen (je Gruppe oder insgesamt) berechnet, die als Liste oder als Diagramm ausgegeben werden können.

Hinweis: Ein Umlegungsergebnis ist nicht mehr zwingend erforderlich für die Ermittlung des Korrelationskoeffizienten.

Tabelle 158 zeigt die Berechnungsvorschriften für die Ausgabeattribute der Umlegungsanalyse. In den Formeln gilt Folgendes:

Z	Beobachtung (Zählung oder Messung)
U	Berechnung (Umlegung oder Netzmodell)
N	Anzahl Objekte mit beobachtetem Wert > 0

AbsRMSE

Abs RMSE

Absolute Wurzel aus mittlerer quadrierter Abweichung

Stärkere Gewichtung signifikanter Differenzen zwischen beobachtetem und berechnetem Wert durch Quadrat nach

Achsabs

Achsenabschnitt

Koeffizient b bei linearer Regression

Siehe Excel, Lineare Regression (y = ax + b)

AnteilAkzGEH

Anteil mit akzept GEH

Anteil Objekte mit akzeptablem GEH-Wert (je Netzobjekt)

AnteilAkzRelFehler

Anteil mit akzept rel Fehler

Anteil Objekte innerhalb der Toleranz

AnzBeob

Anzahl Beobachtungen

Anzahl Beobachtungen je Klasse (Objekte mit beobachteter Wert > 0)

AnzKlasse

Anzahl in Klasse

Gesamtanzahl (= beobachtete + nicht-beobachtete) Objekte je Klasse

KlassenWert

Wert des Klassifizierungsattributs (oder leer, falls nicht klassifiziert)

Korr

Korrelationskoeffizient (Siehe Excel-Funktion Pearson)

Hinweise

Der Wertebereich liegt zwischen -1 und 1, wobei Folgendes gilt:

- 1 = Beobachtung gegenläufig zur Berechnung
0 = nicht korreliert (zufällig)
+1 = sehr gute Korrelation

Das Verhältnis beobachteter/berechneter Wert sollte möglichst nahe 1 sein.

Bei nur zwei Werten > 0 ist der Korrelationskoeffizient -1 oder 1.

Der Wert des Korrelationskoeffizienten erlaubt keine Rückschlüsse darauf, ob entweder alle beobachteten Werte größer (oder kleiner) sind als die berechneten Werte oder ob sowohl Abweichungen nach oben als auch Abweichungen nach unten vorliegen.

MittAbsFehler

Mittlerer absoluter Fehler

Mittlere Abweichung der Absolutwerte (δa)

(Differenz zwischen beobachtetem und berechnetem Wert)